TUTORIALS

How to measure different types of curves in roads

There are 2 sorts of curves in road construction that go from vertical curve as well as horizontal curve.

Horizontal curve: That sort of curve provides a channel amid 2 road tangent strips that assists a means of transport to make a turn at a moderate pace despite a sharp cut.

Furthermore, the horizontal curves are classified as subsequent: Compound Curve, Reverse Curve, Transition Curve and Simple Curve.

Simple Curve: One simple arc is set in the road to place a curve amid the 2 straight lines.

Compound Curve: Arrangement of 2 simple curves that are connected to curve in the same direction.

Reverse Curve: Arrangement of 2 simple curves that are connected together to curve in the other/different/opposite direction.

Transition Curve: One curve that comprises continually varying radius. Moreover, it is implemented to connect a round/circular arc to a linear/straight line.

Vertical Curve: One vertical curve provides a channel amid 2 slanted roads that helps a means of transport to set the elevation rate alteration at a moderate pace despite a sharp cut.

Moreover, the vertical curve is classified as subsequent: Crest Curve, Sag Curve

Sag Curve: Sag curve changes the road alignment from ascending to downwards.

Crest Curve: It changes the road alignment from downwards to ascending.

Circular curve length is computed through the subsequent formula:

  • L = πRØ/180
  • or else L = Ø/360 x 2πr
  • otherwise L = Ø/360 x πD

At this point, L represents the circular curve length:

  • R signifies the circular curve radius.
  • D signifies the circular curve diameter.
  • Ø signifies the deflection or central angle.

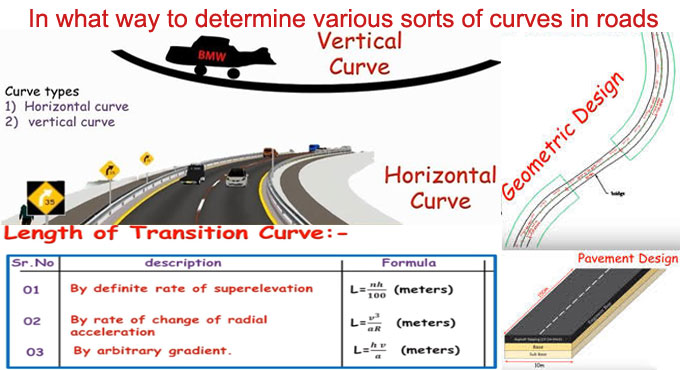
The transition curve Length is computed through the subsequent formula:

Through superelevation definite rate
Formula :– L is equal to nh/100 [meters]
Through rate of change of/change rate of radial acceleration
Formula :– L is equal to v3/aR [meters]
Through arbitrary gradient
Formula :– L is equal to hv/a [meters]

To get more details, go through the following video tutorial.

Lecturer: SL Khan

In what way to determine various sorts of curves in roads