NEWS | SOFTWARE | SHEET
Understanding Flexural Strength in Concrete: Unveiling the Significance in Construction
In the vast realm of construction, various material properties play a pivotal role in determining the structural integrity and longevity of buildings. One such critical parameter is the flexural strength of concrete, a key factor in assessing a material's ability to withstand bending forces.
In this comprehensive exploration, we delve into the intricacies of the modulus of rupture, flexural modulus, and flexural stress, shedding light on their significance in construction and how they collectively contribute to the robustness of concrete structures.
The Basics: Flexural Strength and Its Components
1. Modulus of Rupture
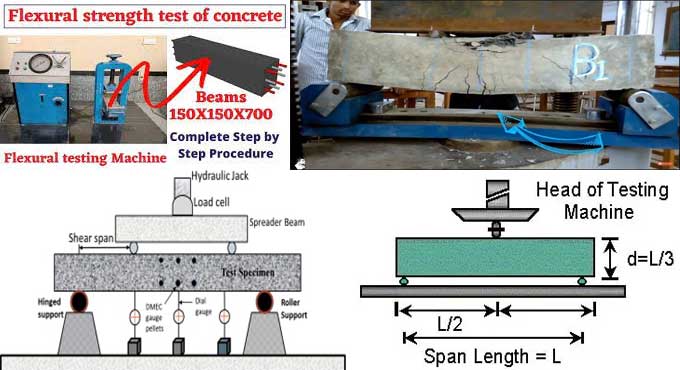
The modulus of rupture (MOR) is a fundamental mechanical property that characterizes the material's resistance to failure under bending or flexural stresses. It is a measure of the maximum stress a material can withstand before fracturing or rupturing when subjected to a bending force. In the context of concrete, the modulus of rupture is a crucial parameter as it reflects the material's ability to endure loads applied perpendicular to its longitudinal axis.
Mathematically, the modulus of rupture is calculated using the formula:
MOR=b.d2P.L
Where:
MOR is the modulus of rupture,
P is the maximum applied load,
L is the span length between supports,
b is the width of the test specimen, and
d is the depth of the test specimen.
Understanding the modulus of rupture is essential for engineers and construction professionals to evaluate the structural adequacy of concrete members subjected to bending forces. This parameter directly influences design considerations and material selection, ensuring that structures can withstand the anticipated loads without compromising safety.
2. Flexural Modulus
While the modulus of rupture assesses the maximum stress a material can endure during bending, the flexural modulus (also known as the modulus of elasticity in bending or bending modulus) provides insights into a material's stiffness under such conditions. In simpler terms, it quantifies how much a material will deform under bending stress without undergoing permanent damage.
The flexural modulus is calculated using the formula:
Where:
E=δ/ϵ
E is the flexural modulus,
δ is the change in stress, and
ϵ is the corresponding change in strain.
This modulus aids in predicting the extent of deflection in a structural element when subjected to bending forces. In the realm of construction, understanding the flexural modulus is crucial for designing elements like beams and slabs, where minimizing deflection is essential for both aesthetic and functional reasons.
3. Flexural Stress
Flexural stress is the stress experienced by a material at the outermost fibers when subjected to a bending force. In the context of concrete, flexural stress is critical in assessing the capacity of structural elements, such as beams and slabs, to withstand applied loads. The distribution of flexural stress across the depth of a concrete member is not uniform, and understanding this stress distribution is vital for designing safe and efficient structures.
Mathematically, flexural stress
σf=M/S
Where:
σf is the flexural stress,
M is the applied moment, and
S is the section modulus of the concrete member.
By evaluating flexural stress, engineers can make informed decisions regarding the appropriate dimensions and reinforcement of structural elements, ensuring that the designed structures meet safety standards and performance criteria.
Significance in Construction
Understanding the significance of modulus of rupture, flexural modulus, and flexural stress in the field of construction is crucial for ensuring the safety, durability, and performance of concrete structures. Here are several key aspects that underscore their importance:
1. Structural Integrity and Safety
The primary goal in construction is to create structures that are not only aesthetically pleasing but also structurally sound and safe. The modulus of rupture plays a pivotal role in this context by providing a measure of the maximum stress a material can withstand. This information is integral to designing structural elements that can support anticipated loads without the risk of failure.
For instance, in the design of beams and slabs, understanding the modulus of rupture allows engineers to determine the required dimensions and reinforcement to ensure that these elements can bear the applied loads without exceeding their capacity. This is vital for preventing catastrophic failures and ensuring the safety of occupants.
2. Material Selection and Quality Control
The choice of construction materials significantly influences the overall performance and longevity of structures. Concrete, being a widely used construction material, must meet stringent quality standards to ensure its reliability in various applications. The modulus of rupture serves as a key parameter in material selection and quality control processes.
Engineers and construction professionals can use the modulus of rupture to assess the quality of concrete batches and verify if they meet the specified design requirements. Monitoring this parameter during material testing and quality control processes helps identify any deviations from the expected performance, allowing for timely adjustments and ensuring that only high-quality materials are used in construction projects.
3. Design Optimization
Efficient design is a cornerstone of successful construction projects. The flexural modulus plays a crucial role in optimizing designs by providing insights into the stiffness of materials under bending stresses. This information is particularly relevant in designing elements like beams, where minimizing deflection is essential for both structural performance and aesthetic considerations.
By understanding the flexural modulus, engineers can make informed decisions about the appropriate material properties and dimensions to achieve the desired balance between strength and flexibility. This optimization not only contributes to the structural efficiency of the design but also influences the overall cost-effectiveness of the construction project.
4. Load Distribution and Serviceability
Structural elements in construction must not only withstand maximum loads but also maintain serviceability under various conditions. Flexural stress analysis is crucial for understanding how loads are distributed across the depth of concrete members. This knowledge is essential for ensuring that elements like beams and slabs remain within acceptable deflection limits and do not compromise the functionality or aesthetics of the structure.
By evaluating flexural stress, engineers can design structures that not only meet safety requirements but also provide satisfactory performance in terms of serviceability. This is particularly important in applications where stringent deflection criteria are specified, such as in the design of floors and other horizontal elements.
To get more details, go through the following video tutorial.
Lecturer: CementPDM
5. Sustainability and Life-Cycle Performance
In the modern era of construction, sustainability is a key consideration in the design and construction of buildings. The choice of materials and the efficiency of designs directly impact the environmental footprint and long-term performance of structures. Understanding the modulus of rupture and flexural modulus contributes to the development of sustainable construction practices.
Optimizing designs based on these parameters allows for the use of materials more efficiently, reducing waste and environmental impact. Additionally, structures designed with a thorough understanding of flexural strength parameters are likely to have longer life cycles, requiring less frequent maintenance and replacement.
Challenges and Future Perspectives
While the modulus of rupture, flexural modulus, and flexural stress provide valuable insights into the behavior of concrete under bending stresses, challenges remain in accurately predicting and modeling these properties. Advances in materials science and testing methodologies continue to refine our understanding of concrete behavior, offering opportunities for more accurate predictions and enhanced design methodologies.
Future research in this field may focus on developing advanced testing techniques, exploring innovative materials, and refining computational models to better predict the flexural behavior of concrete. Additionally, the integration of data-driven approaches and artificial intelligence in material testing and design processes could further revolutionize our ability to optimize structures for performance and sustainability.