NEWS | SOFTWARE | SHEET

Trigonometric Leveling Surveying – Theory and Formulas for Calculations

To find out the vertical distance between two points with the help of certain measurements of the vertical angles and the already known distances we use a branch of surveying called Trigonometric Leveling.

It is assumed thatthe known distances are either horizontal or the geodetic lengths at the mean sea level (MSL). Direct measurement of distance takes place (as in the plane surveying) or just as in geodetic surveying they are computed.

The following two ways by which Trigonometric Leveling can be done:

• Observations taken for the height and distances.
• Geodetic Observations.

In the first type, if accessible the horizontal distance between the given points can be measured.

The observation of the vertical angles is taken into account using which we can compute the distances. The correction for the curvature and refraction must be provided if the distances are large enough and a linearly to the distances is provided that we have computed.

In the second type, which is the geodetic observations, the geodetic distances are the distances between the two points and the principles of the plane surveying are inapplicable here. Directly to the angles the corrections for the curvature and refraction are applied.

Given below are various cases to find out the difference in elevation between the two points:

(1) The distance is known for the Two Points, which means thatthe base of the object is accessible.

By taking the vertical angle observations we can find the distance between the two points present at a known horizontal distance.

By using trigonometry, we can calculate the vertical distance if the vertical angle of elevation from the point to be observed to the instrument axis is known.

Horizontal distance X tangent(vertical angle) = Vertical difference between the two.

There is no need to apply the correction for the curvature and refraction if the points are at a small distance apart if not then you can apply the correction as stated below.
C= 0.06728*D^2

In this case D is the horizontal distance between the given two points measured in Kilometers. But the Correction is in meters (m).

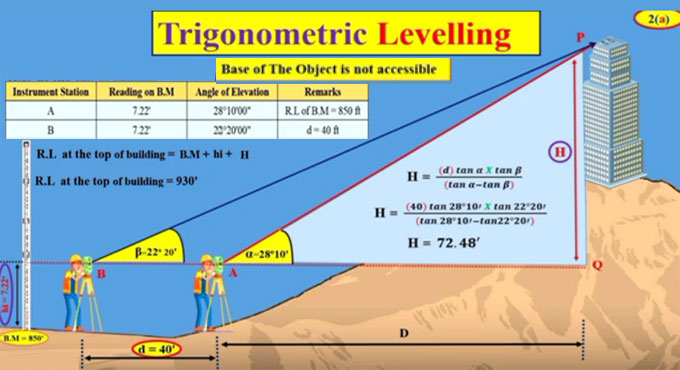
(2) Inaccessible base of the object.

Three different cases are discussed in the sections (a), (b) and (c).

(a) When the observation is taken from the same level of line of sight in case the instrument is shifted to a nearby place.

In this kind of case, two angular observations of the vertical angles must be taken. The vertical difference in distance between the line of sight of the instrument and the top point of the object can be found if the instrument is shifted to a close by plan of know distance and then we can take the help of the known distance between these two and the angular observations from the two stations.

(b) When there is a difference in thelines of sight of the two instrument settings.

There can be two cases for it.

When with the vertical staff readings, the line of sight at a small vertical distancecan be measured.

In case the difference is larger than the staff height.

• In case of the first one, you can apply the formula for the difference in the height of the top of the object from the given two lines of sights. When the staff is kept at a little distance from the two points then that staff reading difference is the same as the difference in lines of sights. Therefore, finding the solution for the vertical distance is easy.
• In case of the second one, it is important to put vane staff at the first instrument station and the angle of elevation is measured from the second point of observation. This will help in finding the difference in the line of the sights between the two points of instrument station.

(c) Third scenario, this is when the instrument station and the top of the object are not in the same vertical plane.

It is important to measure at-least two horizontal angles of the horizontal triangle formed by the two instrument stations and the base of the object.

The sine rule to solve the horizontal distances of the triangle can be applied after the vertical angular observations from the two instrument stations are taken. The vertical distance between the two-point can be calculated with the help of these angles and the distances.

To get more details, go through the following video tutorial.

Lecturer: Civil Engineering ZoNe