TUTORIALS
What is D2/162 and D2/533 in Steel

In this exclusive civil engineering tutorial, you will get information on derivation of D2/162 and D2/533 to find out the unit weight of steel in kg/m3.
- These two equations are utilized for finding the weight of steel bars while the length of steel bars is known.
- The formulas provide the steel weight per unit length.
- The formula (D2/162) is utilized while the length is specified in meters.
- The formula (D2/533) is utilized while the steel bar length is specified in feet.
The formulas provide the quantity of steel bars needed in kg.
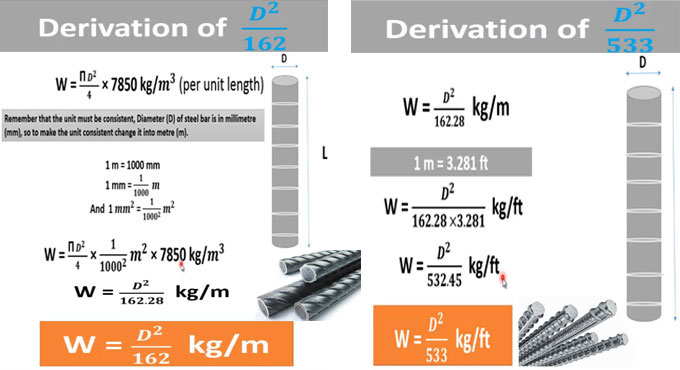
D2/162 Derivation
The steel bar has diameter ‘D’ and length “L”.
Steel weight = Steel bar volume x Steel unit weight
W (Steel weight) = V (Steel bar volume) x γ (Steel unit weight)
V (Steel bar volume) = cross-sectional area of steel bar x Length = A x L
W = A x L x γ
W = πD2/4 x γ
As steel unit weight (γ) in MKS system is 7850 kg/m3
W = πD2/4 x 7850 kg/m3 [per unit length]
Take into consideration that unit should be constant; steel bar diameter (D) is in millimetre (mm), in order to make the unit uniform, alter it into meter (m).
One meter = One thousand mm
1 mm = 1/1000 m
1 mm2 = 1/ (1000)2 m2
W = πD2/4 x 1/ (1000)2 m2 x 7850 kg/m3
W = D2/162.28 kg/m
W = D2/162 kg/m
Take into consideration that the formula will provide the steel bar weight in kg/m.
Multiply it by steel bar length (L) in order to find out the steel bar weight.
D2/533 Derivation
W = D2/162 kg/m
1 m = 3.281 ft
W = D2/162 x 3.281 kg/ft
W = D2/532.45 kg/ft
W = D2/533 kg/ft
Take into consideration that W = D2/162 kg/m is utilized when the bar length is specified in m.
W = D2/533 kg/ft is utilized when the bar length is specified in ft.
Watch the following video to learn the complete process.
Lecturer: Civil Engineering World - THE CIVILOIDS